R中的探索性因素分析

什么是R中的探索性因素分析？

探索性因子分析 (EFA) 或在 R 中粗略地称为因子分析是一种统计技术，用于识别一组变量之间的潜在关系结构并将其缩小到较少数量的变量。 这实质上意味着大量变量的方差可以用几个汇总变量即因子来描述。 这是R中探索性因子分析的概述。

顾名思义，EFA 本质上是探索性的——我们并不真正了解潜在变量，并且重复这些步骤，直到我们得到较少数量的因子。 在本教程中，我们将使用 R 来了解 EFA。现在，让我们首先了解数据集的基本概念。

1. 数据

该数据集包含客户在购买汽车时考虑的 14 个不同变量的 90 个响应。 调查问题采用 5 点李克特量表，1 表示非常低，5 表示非常高。 变量如下：

• 价格
• 安全
• 外观
• 空间和舒适
• 技术
• 售后服务
• 转售价值
• 汽油种类
• 燃油效率
• 颜色
• 维护
• 试驾
• 产品评论
• 感言

单击此处下载编码数据集。

2. 导入WebData

现在我们将以 CSV 格式存在的数据集读入 R 并将其存储为变量。

[代码语言=“r”]数据<-read.csv(file.choose( ),header=TRUE) [/code]

它将打开一个窗口来选择 CSV 文件，并且 `header` 选项将确保文件的第一行被视为标题。 输入以下内容，查看数据框的前几行，并确认数据已正确存储。

[代码语言=“r”]头（数据）[/code]

3.包安装

现在我们将安装所需的包以进行进一步的分析。 这些包是 `psych` 和 `GParotation`。 在下面给出的代码中，我们调用 `install.packages()` 进行安装。

[代码语言=”r”] install.packages('psych') install.packages('GPRotation') [/code]

4. 因素的数量

接下来，我们将找出我们将为因子分析选择的因子数量。 这是通过“并行分析”和“特征值”等方法进行评估的。

平行分析

我们将使用 `Psych` 包的 `fa.parallel` 函数来执行并​​行分析。 这里我们指定数据框和因子方法（在我们的例子中是`minres`）。 运行以下命令以找到可接受的因子数并生成“碎石图”：

[代码语言=“r”]并行<- fa.parallel(data, fm = 'minres', fa = 'fa') [/code]

控制台将显示我们可以考虑的最大因素数。 这是它的外观。

“平行分析表明因子数 = 5，成分数 = NA”

在上面代码生成的“碎石图”中给出如下：

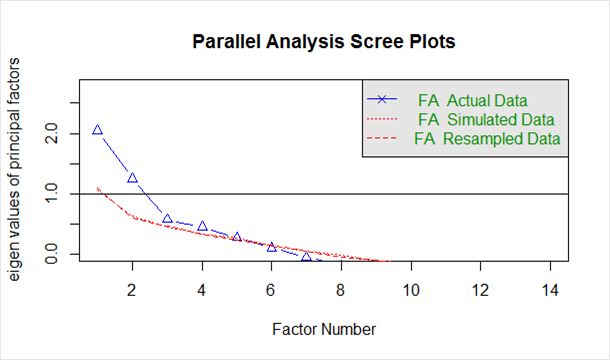
蓝线显示实际数据的特征值，两条红线（相互重叠）显示模拟和重采样数据。 在这里，我们查看实际数据中的大幅下降，并发现它向右稳定的点。 此外，我们找到了拐点——模拟数据和实际数据之间的差距趋于最小的点。

查看此图和平行分析，2 到 5 个因素之间的任何地方都是不错的选择。

因子分析

现在我们已经得出了可能的因子数，让我们从 3 作为因子数开始。 为了执行因子分析，我们将使用 `psych` 包`fa() 函数。 以下是我们将提供的论点：

• r - 原始数据或相关或协方差矩阵
• nfactors – 要提取的因子数
• rotate - 虽然有各种类型的旋转，但 `Varimax` 和 `Oblimin` 是最受欢迎的
• fm – 因子提取技术之一，如“最小残差 (OLS)”、“最大似然”、“主轴”等。

在这种情况下，我们将选择倾斜旋转（rotate = “oblimin”），因为我们认为这些因素之间存在相关性。 请注意，在假设因子完全不相关的情况下使用 Varimax 旋转。 我们将使用“普通最小二乘/最小二乘”因式分解（fm = “minres”），因为众所周知，它可以在不假设多元正态分布的情况下提供类似于“最大似然”的结果，并通过像主轴一样的迭代特征分解得出解。

运行以下命令开始分析。

[代码语言=“r”]三因素<-fa(data,nfactors = 3, rotate = “oblimin”,fm=”minres”) print(threefactor) [/code]

这是显示因子和载荷的输出：

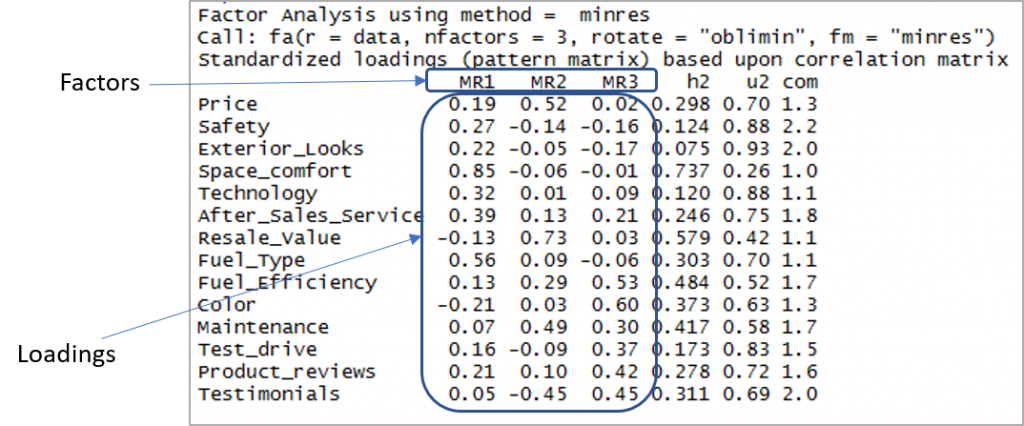
现在我们需要考虑超过 0.3 的载荷，而不是超过一个因素的载荷。 请注意，这里可以接受负值。 因此，让我们首先建立分界线以提高可见性。

[代码语言=“r”] print(threefactor$loadings,cutoff = 0.3) [/code]

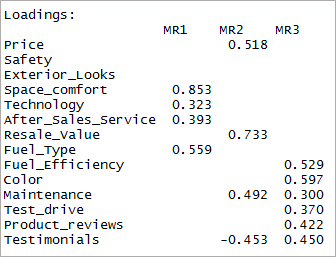
如您所见，两个变量变得微不足道，另外两个变量具有双重加载。 接下来，我们将考虑“4”因素。

[代码语言=“r”]四因素<-fa(data,nfactors = 4, rotate = “oblimin”,fm=”minres”) print(fourfactor$loadings,cutoff = 0.3) [/code]

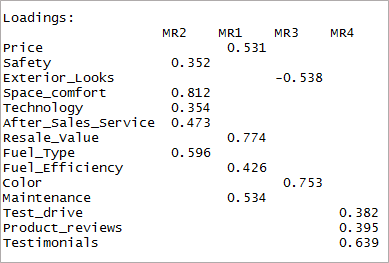
我们可以看到它只导致单次加载。 这被称为简单结构。

点击以下查看因子映射。

[代码语言=“r”] fa.diagram(fourfactor) [/code]

充分性测试

现在我们已经实现了一个简单的结构，是时候验证我们的模型了。 让我们看一下因子分析输出以继续。

根表示残差平方 (RMSR) 为 0.05。 这是可以接受的，因为这个值应该更接近于 0。接下来，我们应该检查 RMSEA（近似的均方根误差）指数。 它的值 0.001 表明模型拟合良好，因为它低于 0.05。 最后，Tucker-Lewis 指数 (TLI) 为 0.93——考虑到它超过 0.9，这是一个可接受的值。

命名因素

在确定因素的充分性之后，是时候为因素命名了。 这是分析的理论方面，我们根据可变载荷形成因子。 在这种情况下，这是如何创建因子的。

结论

在本 r 分析教程中，我们讨论了 EFA（R 中的探索性因子分析）的基本思想，涵盖了并行分析和碎石图解释。 然后我们转移到 R 中的因子分析以实现简单的结构并对其进行验证以确保模型的充分性。 最后从变量中得出因素的名称。 现在继续，尝试一下，并将您的发现发布在评论部分。