Analisi fattoriale esplorativa in R

Che cos'è l'analisi fattoriale esplorativa in R?

L'analisi fattoriale esplorativa (EFA) o più o meno nota come analisi fattoriale in R è una tecnica statistica utilizzata per identificare la struttura relazionale latente tra un insieme di variabili e restringerla a un numero inferiore di variabili. Ciò significa essenzialmente che la varianza di un gran numero di variabili può essere descritta da poche variabili riassuntive, cioè fattori. Ecco una panoramica dell'analisi fattoriale esplorativa in R.

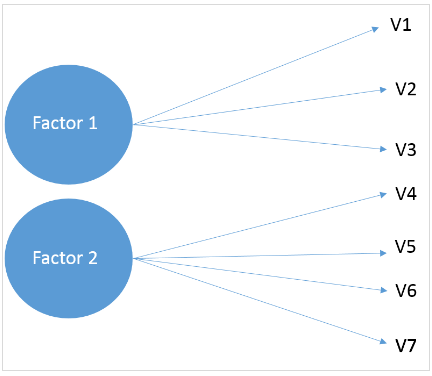
Come suggerisce il nome, l'EFA è di natura esplorativa: non conosciamo davvero le variabili latenti e i passaggi vengono ripetuti finché non arriviamo a un numero inferiore di fattori. In questo tutorial, esamineremo EFA usando R. Ora, per prima cosa, prendiamo l'idea di base del set di dati.

1. I dati

Questo set di dati contiene 90 risposte per 14 diverse variabili che i clienti considerano durante l'acquisto di un'auto. Le domande del sondaggio sono state inquadrate utilizzando una scala Likert a 5 punti con 1 molto basso e 5 molto alto. Le variabili erano le seguenti:

• Prezzo
• Sicurezza
• Aspetto esteriore
• Spazio e comfort
• Tecnologia
• Assistenza post-vendita
• Valore di rivendita
• Tipo di carburante
• Efficienza del carburante
• Colore
• Manutenzione
• Test di guida
• Recensioni dei prodotti
• Testimonianze

Fare clic qui per scaricare il set di dati codificato.

2. Importazione di dati Web

Ora leggeremo il set di dati presente in formato CSV in R e lo memorizzeremo come variabile.

[code language=”r”] dati <- read.csv(file.choose( ),header=TRUE) [/codice]

Si aprirà una finestra per scegliere il file CSV e l'opzione `header` assicurerà che la prima riga del file sia considerata come intestazione. Immettere quanto segue per visualizzare le prime righe del frame di dati e confermare che i dati sono stati memorizzati correttamente.

[code language=”r”] head(data) [/code]

3. Installazione del pacchetto

Ora installeremo i pacchetti richiesti per eseguire ulteriori analisi. Questi pacchetti sono `psych` e `GPArotation`. Nel codice riportato di seguito, chiamiamo `install.packages()` per l'installazione.

[code language=”r”] install.packages('psych') install.packages('GPArotation') [/code]

4. Numero di fattori

Successivamente, scopriremo il numero di fattori che selezioneremo per l'analisi fattoriale. Questo viene valutato tramite metodi come "Analisi parallela" e "autovalore", ecc.

Analisi Parallela

Useremo la funzione `fa.parallel` del pacchetto `Psych` per eseguire l'analisi parallela. Qui specifichiamo il frame di dati e il metodo del fattore (`minres` nel nostro caso). Eseguire quanto segue per trovare un numero accettabile di fattori e generare lo "scree plot":

[code language=”r”] parallelo <- fa.parallel(data, fm = 'minres', fa = 'fa') [/code]

La console mostrerebbe il numero massimo di fattori che possiamo considerare. Ecco come sarebbe.

"L'analisi parallela suggerisce che il numero di fattori = 5 e il numero di componenti = NA"

Dato di seguito nello "scree plot" generato dal codice sopra:

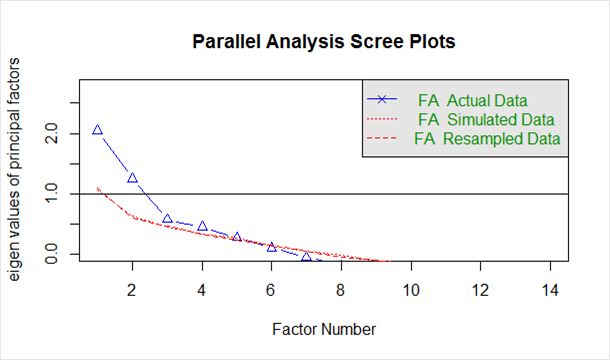
La linea blu mostra gli autovalori dei dati effettivi e le due linee rosse (poste una sopra l'altra) mostrano i dati simulati e ricampionati. Qui osserviamo i grandi cali nei dati effettivi e individuiamo il punto in cui si livella a destra. Inoltre, individuiamo il punto di flesso, il punto in cui il divario tra dati simulati e dati effettivi tende ad essere minimo.

Osservando questo grafico e l'analisi parallela, da 2 a 5 fattori sarebbe una buona scelta.

Analisi fattoriale

Ora che siamo arrivati ​​a un numero probabile di fattori, iniziamo con 3 come numero di fattori. Per eseguire l'analisi fattoriale, useremo la funzione `psych` packages`fa(). Di seguito sono riportati gli argomenti che forniremo:

• r – Dati grezzi o matrice di correlazione o covarianza
• nfactors – Numero di fattori da estrarre
• ruotare – Sebbene ci siano vari tipi di rotazioni, `Varimax` e `Oblimin` sono le più popolari
• fm – Una delle tecniche di estrazione dei fattori come `Minimum Residual (OLS)`, `Maximum Liklihood`, `Principal Axis` ecc.

In questo caso, selezioneremo la rotazione obliqua (ruota = "oblimin") poiché riteniamo che ci sia una correlazione tra i fattori. Si noti che la rotazione Varimax viene utilizzata presupponendo che i fattori siano completamente non correlati. Utilizzeremo la fattorizzazione `Ordinary Least Squared/Minres` (fm = “minres”), poiché è noto che fornisce risultati simili a `Massima verosimiglianza` senza assumere una distribuzione normale multivariata e deriva soluzioni attraverso una eigedecomposizione iterativa come un asse principale.

Eseguire quanto segue per avviare l'analisi.

[code language=”r”] tre fattori <- fa(data,nfactors = 3, ruotare = “oblimin”,fm=”minres”) print(tre fattori) [/codice]

Ecco l'output che mostra fattori e carichi:

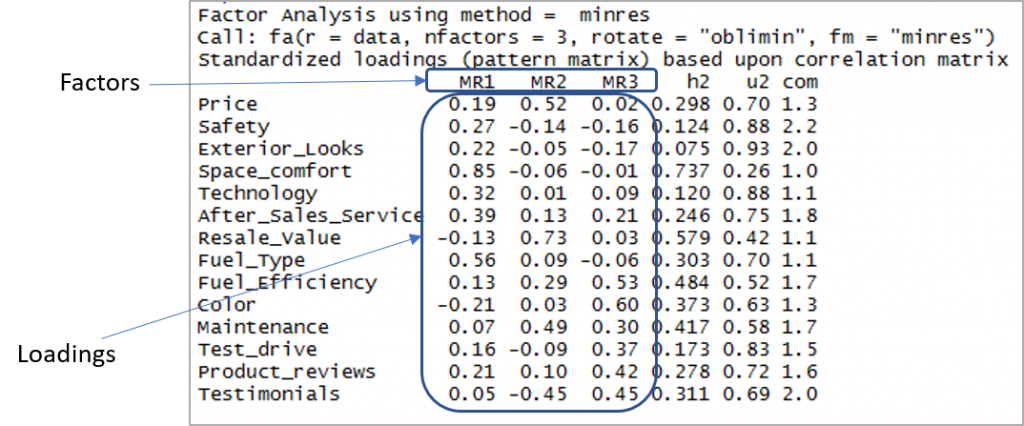
Ora dobbiamo considerare i caricamenti superiori a 0,3 e non il caricamento su più di un fattore. Si noti che i valori negativi sono accettabili qui. Quindi stabiliamo prima il cut-off per migliorare la visibilità.

[code language=”r”] print(threefactor$loadings,cutoff = 0.3) [/code]

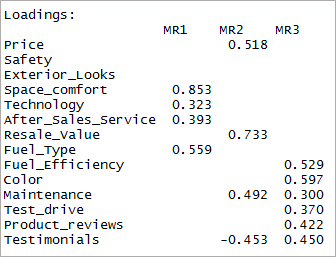
Come puoi vedere due variabili sono diventate insignificanti e altre due hanno un doppio caricamento. Successivamente, considereremo i fattori "4".

[code language=”r”] fourfactor <- fa(data,nfactors = 4, rotate = “oblimin”,fm=”minres”) print(fourfactor$loadings,cutoff = 0.3) [/code]

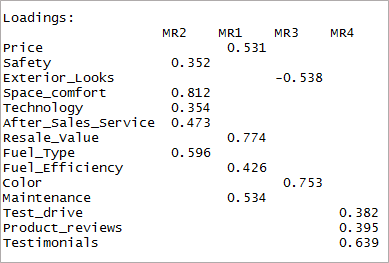
Possiamo vedere che si traduce in un solo caricamento singolo. Questa è nota come struttura semplice.

Premi quanto segue per guardare la mappatura dei fattori.

[code language=”r”] fa.diagram(fourfactor) [/code]

Prova di adeguatezza

Ora che abbiamo ottenuto una struttura semplice, è giunto il momento di convalidare il nostro modello. Diamo un'occhiata all'output dell'analisi fattoriale per procedere.

La radice significa che il quadrato dei residui (RMSR) è 0,05. Questo è accettabile in quanto questo valore dovrebbe essere più vicino a 0. Successivamente, dovremmo controllare l'indice RMSEA (errore quadratico medio dell'approssimazione). Il suo valore, 0,001, mostra un buon adattamento del modello in quanto è inferiore a 0,05. Infine, il Tucker-Lewis Index (TLI) è 0,93, un valore accettabile considerando che è superiore a 0,9.

Denominare i fattori

Dopo aver stabilito l'adeguatezza dei fattori, è il momento di nominare i fattori. Questo è il lato teorico dell'analisi in cui formiamo i fattori che dipendono dai carichi variabili. In questo caso, ecco come si possono creare i fattori.

Conclusione

In questo tutorial per l'analisi in r, abbiamo discusso l'idea di base di EFA (analisi fattoriale esplorativa in R), l'analisi parallela coperta e l'interpretazione dello scree plot. Quindi siamo passati all'analisi fattoriale in R per ottenere una struttura semplice e convalidare la stessa per garantire l'adeguatezza del modello. Finalmente sono arrivati ​​i nomi dei fattori dalle variabili. Ora vai avanti, provalo e pubblica i tuoi risultati nella sezione commenti.