Analiza factorială exploratorie în R

Ce este analiza factorială exploratorie în R?

Analiza factorială exploratorie (EFA) sau aproximativ cunoscută ca analiza factorială în R este o tehnică statistică care este utilizată pentru a identifica structura relațională latentă între un set de variabile și pentru a o restrânge la un număr mai mic de variabile. Aceasta înseamnă în esență că varianța unui număr mare de variabile poate fi descrisă prin câteva variabile rezumative, adică factori. Iată o prezentare generală a analizei factorilor exploratorii în R.

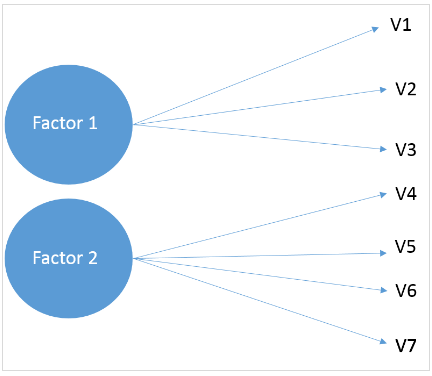
După cum sugerează și numele, EFA este de natură exploratorie – nu cunoaștem cu adevărat variabilele latente, iar pașii se repetă până ajungem la un număr mai mic de factori. În acest tutorial, ne vom uita la EFA folosind R. Acum, să obținem mai întâi ideea de bază a setului de date.

1. Datele

Acest set de date conține 90 de răspunsuri pentru 14 variabile diferite pe care clienții le iau în considerare atunci când cumpără o mașină. Întrebările sondajului au fost încadrate folosind o scală Likert cu 5 puncte, 1 fiind foarte scăzut și 5 foarte mare. Variabilele au fost următoarele:

• Preț
• Siguranță
• Aspecte exterioare
• Spațiu și confort
• Tehnologie
• Service post-vânzare
• Valoarea de revânzare
• Tipul combustibilului
• Eficienta consumului de combustibil
• Culoare
• întreținere
• Test drive
• Recenzii de produse
• Mărturii

Faceți clic aici pentru a descărca setul de date codificat.

2. Importul WebData

Acum vom citi setul de date prezent în format CSV în R și îl vom stoca ca variabilă.

[limba codului=”r”] date &;lt;-read.csv(fișier.alege( ),header=TRUE) [/code]

Se va deschide o fereastră pentru a alege fișierul CSV și opțiunea `header` se va asigura că primul rând al fișierului este considerat antet. Introduceți următoarele pentru a vedea primele rânduri ale cadrului de date și pentru a confirma că datele au fost stocate corect.

[code language=”r”] head(data) [/code]

3. Instalarea pachetului

Acum vom instala pachetele necesare pentru a efectua analize suplimentare. Aceste pachete sunt `psych` și `GPRotation`. În codul de mai jos, apelăm `install.packages()` pentru instalare.

[code language=”r”] install.packages('psych') install.packages('GPRotation') [/code]

4. Numărul de factori

În continuare, vom afla numărul de factori pe care îi vom selecta pentru analiza factorială. Aceasta este evaluată prin metode precum „Analiza paralelă” și „Valoare proprie”, etc.

Analiza paralelă

Vom folosi funcția `fa.parallel` a pachetului `Psych` pentru a executa analiza paralelă. Aici specificăm cadrul de date și metoda factorului (`minres` în cazul nostru). Rulați următoarele pentru a găsi un număr acceptabil de factori și generați „scree plot”:

[Limbajul codului=”r”] paralel &;lt;-fa.parallel(data, fm = 'minres', fa = 'fa') [/code]

Consola ar arăta numărul maxim de factori pe care îi putem lua în considerare. Iată cum ar arăta.

„Analiza paralelă sugerează că numărul de factori = 5 și numărul de componente = NA“

Dat mai jos în „scree plot” generat din codul de mai sus:

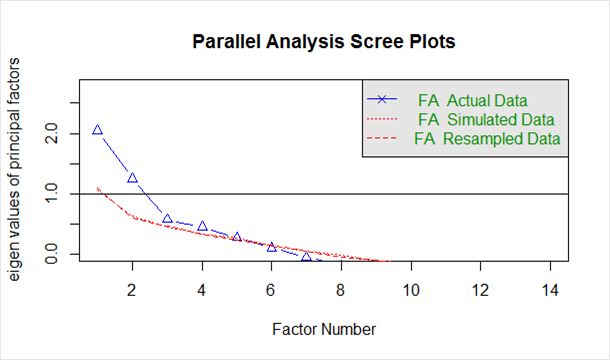
Linia albastră arată valorile proprii ale datelor reale, iar cele două linii roșii (plasate una peste alta) arată datele simulate și reeșantionate. Aici ne uităm la scăderile mari ale datelor reale și găsim punctul în care se nivelează la dreapta. De asemenea, localizăm punctul de inflexiune – punctul în care decalajul dintre datele simulate și datele reale tinde să fie minim.

Privind acest complot și analiza paralelă, între 2 și 5 factori ar fi o alegere bună.

Analiza factorilor

Acum că am ajuns la un număr probabil de factori, să începem cu 3 ca număr de factori. Pentru a efectua analiza factorială, vom folosi funcția `psych` packages`fa(). Mai jos sunt prezentate argumentele pe care le vom furniza:

• r – Date brute sau matrice de corelație sau covarianță
• nfactors – Numărul de factori de extras
• rotiți – Deși există diferite tipuri de rotații, `Varimax` și `Oblimin` sunt cele mai populare
• fm – Una dintre tehnicile de extracție a factorilor precum `Reziduul minim (OLS)`, `Probabilitatea maximă`, `Axa principală` etc.

În acest caz, vom selecta rotația oblică (rotate = „oblimin”) deoarece credem că există o corelație între factori. Rețineți că rotația Varimax este utilizată în ipoteza că factorii sunt complet necorelați. Vom folosi factorizarea „Ordinary Least Squared/Minres” (fm = „minres”), deoarece se știe că oferă rezultate similare cu „Maximum Likelihood” fără a presupune o distribuție normală multivariată și derivă soluții prin compunerea propriu-zisă iterativă ca o axă principală.

Rulați următoarele pentru a începe analiza.

[Limbajul codului=”r”] trei factori <- fa(data,nfactors = 3, rotire = „oblimin”,fm="minres”) print(trei factori) [/code]

Iată rezultatul care arată factorii și încărcările:

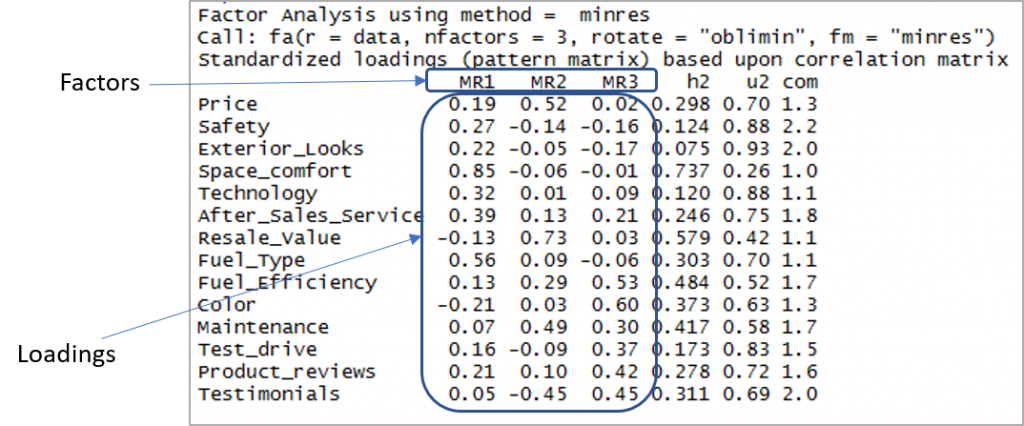
Acum trebuie să luăm în considerare încărcările mai mari de 0,3 și nu încărcările pe mai mult de un factor. Rețineți că valorile negative sunt acceptabile aici. Deci, să stabilim mai întâi limita pentru a îmbunătăți vizibilitatea.

[code language=”r”] print(trei factori $încărcări, cutoff = 0,3) [/code]

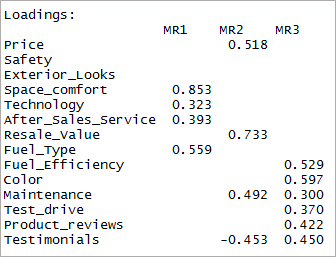
După cum puteți vedea, două variabile au devenit nesemnificative și alte două au încărcare dublă. În continuare, vom lua în considerare cei „4” factori.

[Limbajul codului=”r”] fourfactor &;amp;;lt;-fa(data,nfactors = 4, rotire = „oblimin”,fm="minres”) print(fourfactor$loadings,cutoff = 0.3) [/code]

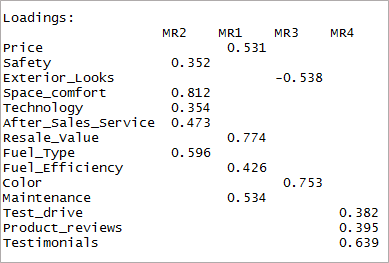
Putem vedea că rezultă doar o singură încărcare. Aceasta este cunoscută sub numele de structură simplă.

Apăsați următoarele pentru a vedea maparea factorilor.

[code language=”r”] fa.diagram(fourfactor) [/code]

Testul de adecvare

Acum că am realizat o structură simplă, este timpul să ne validăm modelul. Să ne uităm la rezultatul analizei factoriale pentru a continua.

Rădăcina înseamnă că pătratul reziduurilor (RMSR) este 0,05. Acest lucru este acceptabil deoarece această valoare ar trebui să fie mai aproape de 0. În continuare, ar trebui să verificăm indicele RMSEA (root mean square error of aproximation). Valoarea sa, 0,001, arată o potrivire bună a modelului, deoarece este sub 0,05. În cele din urmă, indicele Tucker-Lewis (TLI) este 0,93 – o valoare acceptabilă având în vedere că este peste 0,9.

Numirea factorilor

După ce am stabilit caracterul adecvat al factorilor, este timpul să numim factorii. Aceasta este partea teoretică a analizei în care formăm factorii în funcție de încărcările variabile. În acest caz, iată cum pot fi creați factorii.

Concluzie

În acest tutorial pentru analiză în r, am discutat ideea de bază a EFA (analiza factorială exploratorie în R), am analizat analiza paralelă și interpretarea graficului scree. Apoi am trecut la analiza factorială în R pentru a realiza o structură simplă și a valida aceeași pentru a asigura adecvarea modelului. În cele din urmă, am ajuns la numele factorilor din variabile. Acum, continuă, încearcă și postează descoperirile tale în secțiunea de comentarii.