Eksploracyjna analiza czynnikowa w R

Czym jest eksploracyjna analiza czynnikowa w R?

Eksploracyjna analiza czynnikowa (EFA) lub z grubsza znana jako analiza czynnikowa w R to technika statystyczna, która służy do identyfikacji ukrytej struktury relacyjnej wśród zestawu zmiennych i zawężenia jej do mniejszej liczby zmiennych. Oznacza to zasadniczo, że wariancję dużej liczby zmiennych można opisać kilkoma zmiennymi sumarycznymi, tj. czynnikami. Oto przegląd eksploracyjnej analizy czynnikowej w R.

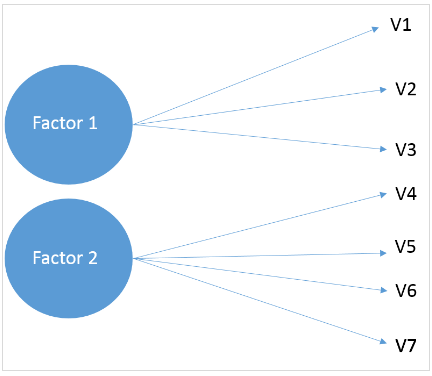
Jak sama nazwa wskazuje, EFA ma charakter eksploracyjny – tak naprawdę nie znamy ukrytych zmiennych, a kroki są powtarzane, dopóki nie osiągniemy mniejszej liczby czynników. W tym samouczku przyjrzymy się EFA przy użyciu R. Teraz najpierw zapoznajmy się z podstawową ideą zestawu danych.

1. Dane

Ten zbiór danych zawiera 90 odpowiedzi dla 14 różnych zmiennych, które klienci biorą pod uwagę przy zakupie samochodu. Pytania ankiety zostały sformułowane przy użyciu 5-stopniowej skali Likerta, gdzie 1 oznacza bardzo niski, a 5 bardzo wysoki. Zmienne były następujące:

• Cena £
• Bezpieczeństwo
• Wygląd zewnętrzny
• Przestrzeń i wygoda
• Technologia
• Serwis pogwarancyjny
• Wartość odsprzedaży
• Typ paliwa
• Efektywność paliwowa
• Kolor
• Konserwacja
• Jazda testowa
• Recenzje produktu
• Referencje

Kliknij tutaj, aby pobrać zakodowany zbiór danych.

2. Importowanie danych internetowych

Teraz wczytamy zbiór danych w formacie CSV do R i zapiszemy go jako zmienną.

[język kodu=”r”] dane i amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;- read.csv(file.choose( ),nagłówek=PRAWDA) [/kod]

Otworzy się okno wyboru pliku CSV, a opcja `header` upewni się, że pierwszy wiersz pliku jest traktowany jako nagłówek. Wprowadź poniższe, aby zobaczyć kilka pierwszych wierszy ramki danych i potwierdzić, że dane zostały poprawnie zapisane.

[język kodu=”r”] nagłówek(dane) [/kod]

3. Instalacja pakietu

Teraz zainstalujemy wymagane pakiety, aby przeprowadzić dalszą analizę. Te pakiety to `psych` i `GPArotation`. W poniższym kodzie wywołujemy `install.packages()` w celu instalacji.

[język kodu=”r”] install.packages('psych') install.packages('GPArotation') [/code]

4. Liczba czynników

Następnie dowiemy się, ile czynników będziemy wybierać do analizy czynnikowej. Jest to oceniane za pomocą metod takich jak „Analiza równoległa” i „wartość własna” itp.

Analiza równoległa

Do przeprowadzenia analizy równoległej użyjemy funkcji `fa.parallel` pakietu `Psych`. Tutaj określamy ramkę danych i metodę współczynnika (w naszym przypadku `minres`). Uruchom następujące polecenie, aby znaleźć akceptowalną liczbę czynników i wygenerować „wykres osypiska”:

[język kodu=”r”] równoległy <- fa.parallel(dane, fm = „minres”, fa = „fa”) [/kod]

Konsola pokazałaby maksymalną liczbę czynników, które możemy wziąć pod uwagę. Oto jak by to wyglądało.

„Analiza równoległa sugeruje, że liczba czynników = 5, a liczba składników = NA”

Podane poniżej w `scree plot` wygenerowanym z powyższego kodu:

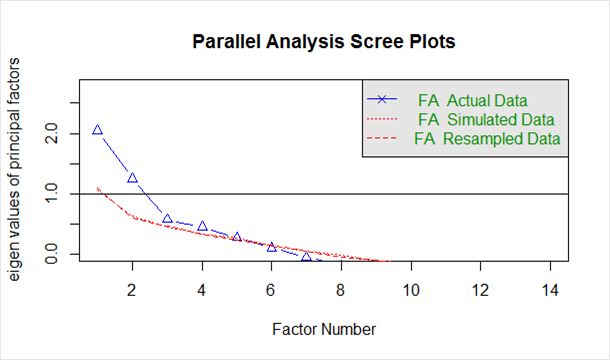
Niebieska linia przedstawia wartości własne rzeczywistych danych, a dwie czerwone linie (umieszczone jedna na drugiej) przedstawiają dane symulowane i ponownie próbkowane. Tutaj przyglądamy się dużym spadkom rzeczywistych danych i zauważamy punkt, w którym następuje wyrównanie po prawej stronie. Ponadto lokalizujemy punkt przegięcia – punkt, w którym różnica między danymi symulowanymi a rzeczywistymi jest zwykle minimalna.

Patrząc na ten wykres i równoległą analizę, dobrym wyborem byłoby od 2 do 5 czynników.

Analiza czynników

Teraz, gdy doszliśmy do prawdopodobnej liczby czynników, zacznijmy od 3 jako liczby czynników. Aby przeprowadzić analizę czynnikową, użyjemy funkcji `psych` packages`fa(). Poniżej przedstawiamy argumenty, które podamy:

• r – Surowe dane lub macierz korelacji lub kowariancji
• nczynniki – Liczba czynników do wyodrębnienia
• rotate – Chociaż istnieją różne rodzaje rotacji, najbardziej popularne są `Varimax` i `Oblimin`
• fm – Jedna z technik ekstrakcji czynników, takich jak „Minimum Residual (OLS)”, „Maximum Liklihood”, „Principal Axis” itp.

W tym przypadku wybierzemy rotację ukośną (obróć = „oblimin”), ponieważ uważamy, że istnieje korelacja między czynnikami. Zauważ, że rotacja Varimax jest używana przy założeniu, że czynniki są całkowicie nieskorelowane. Użyjemy faktoringu „Zwykłe najmniejsze kwadraty/Minres” (fm = „minres”), ponieważ wiadomo, że zapewnia wyniki podobne do „Maksymalnego prawdopodobieństwa” bez zakładania wielowymiarowego rozkładu normalnego i wyprowadza rozwiązania poprzez iteracyjną dekompozycję własną jak oś główna.

Uruchom następujące, aby rozpocząć analizę.

[język kodu=”r”] trzyczynnikowy i wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;wzmacniacz;lt; rotate = „oblimin”,fm=”minres”) print(trzyczynnik) [/kod]

Oto dane wyjściowe pokazujące czynniki i obciążenia:

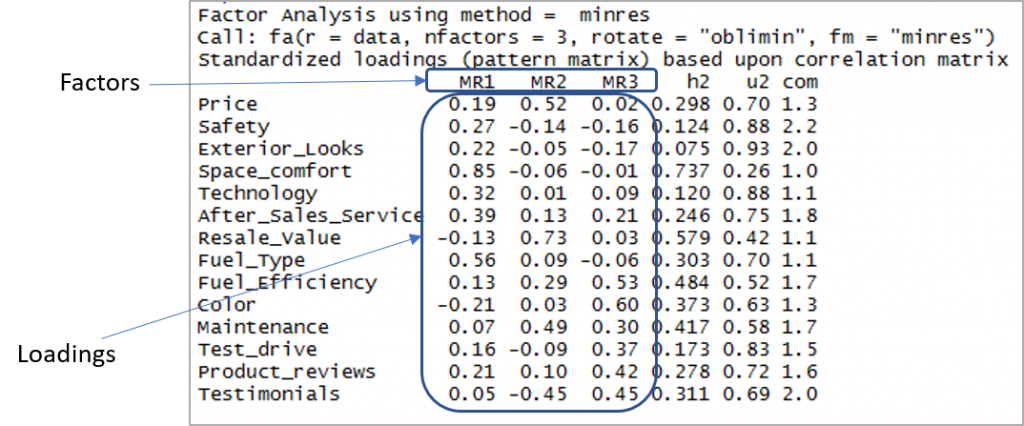
Teraz musimy wziąć pod uwagę ładunki większe niż 0,3 i nie obciążające więcej niż jednego czynnika. Pamiętaj, że dopuszczalne są tutaj wartości ujemne. Więc najpierw ustalmy odcięcie, aby poprawić widoczność.

[język kodu=”r”] print(threefactor$loadings,cutoff = 0.3) [/code]

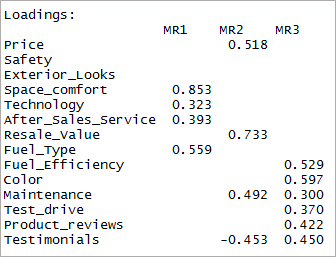
Jak widać dwie zmienne stały się nieistotne, a dwie inne mają podwójne ładowanie. Następnie rozważymy czynniki „4”.

[język kodu=”r”] czteroczynnikowy <- fa(dane,nfactors = 4, rotate = „oblimin”,fm=”minres”) print(czteryfactor$loadings,cutoff = 0.3) [/kod]

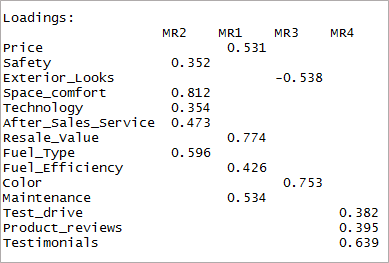
Widzimy, że skutkuje to tylko jednorazowym załadunkiem. Nazywa się to prostą strukturą.

Uderz w poniższe, aby przyjrzeć się mapowaniu czynników.

[język kodu=”r”] fa.diagram(czteroczynnik) [/kod]

Test adekwatności

Teraz, gdy osiągnęliśmy prostą strukturę, nadszedł czas, abyśmy zweryfikowali nasz model. Spójrzmy na wynik analizy czynnikowej, aby kontynuować.

Pierwiastek oznacza, że ​​kwadrat reszt (RMSR) wynosi 0,05. Jest to akceptowalne, ponieważ wartość ta powinna być bliższa 0. Następnie należy sprawdzić wskaźnik RMSEA (średniokwadratowy błąd aproksymacji). Jego wartość 0,001 wskazuje na dobre dopasowanie modelu, ponieważ wynosi poniżej 0,05. Wreszcie indeks Tuckera-Lewisa (TLI) wynosi 0,93 – akceptowalna wartość, biorąc pod uwagę, że przekracza 0,9.

Nazywanie czynników

Po ustaleniu adekwatności czynników nadszedł czas, abyśmy nazwali czynniki. Jest to teoretyczna strona analizy, w której tworzymy czynniki w zależności od obciążeń zmiennych. W tym przypadku, oto jak można tworzyć czynniki.

Wniosek

W tym samouczku do analizy w r omówiliśmy podstawową ideę EFA (eksploracyjnej analizy czynnikowej w R), obejmując analizę równoległą i interpretację wykresu osypiska. Następnie przeszliśmy do analizy czynnikowej w R, aby uzyskać prostą strukturę i zweryfikować ją, aby zapewnić adekwatność modelu. Wreszcie doszliśmy do nazw czynników ze zmiennych. Teraz śmiało, wypróbuj i opublikuj swoje odkrycia w sekcji komentarzy.